C - 자료구조 통곡의 벽 연습 문제 풀이
2022. 3. 30. 16:31ㆍC
1.
//팩토리얼을 계산하는 순환호출 함수 factorial에서 매개 변수로 5를 주었다면
//최대 몇개의 factorial 함수의 활성 레코드가 동시에 존재할 수 있는가?//정답은 5개이다
factorial(5) -> factorial(4) -> factorial(3) -> factorial(2) -> factorial(1)
//순으로 호출하고 f(1)부터 차례대로 함수를 종료하기에 5개가 맞다2.
//순환 호출을 하였을 경우에 활성 레코드들이 저장되는 위치는 스택이다3.
//활성 레코드에 저장되지 않는 것은 무엇인가?
//하나의 함수가 자기자신을 다시 호출하는 것은 다른 함수를 호출하는 것과 동일하다.
//복귀주소가 시스템 스택에 저장되고 호출되는 함수를 위한 매개변수와 지역 변수를
//스택으로 할당 받는다.
//고로 순환호출의 순차번호는 활성레코드에 저장되지 않는다.4.
//하나의 함수가 호출할 수 있는 순환호출의 개수는 스택이 허용하는 한도까지만
//활성레코드가 존재할 수 있다.5.
//다음 순환호출 함수에서 잘못된 점은 무엇인가?
int recursive(int n)
{
if(n==1) return 0;
return n*recursive(n)
}
//순환함수의 종료조건이 제대로 지정되어 있지 않다. n이 1이 아닌 경우 무한히 호출하게 된다.6.
//다음의 순환호출 함수에서 잘못된 점은 무엇인가?
int recursive(int n)
{
printf("recrusive(%d)\n", n);
return n*recursive(n-1);
}
//함수가 끝나지 않고 계속해서 호출한다. 종료조건이 제대로 설정 되어 있지 않다.7.
//다음 함수를 sum(5)로 호출하였을 때, 화면에 출력되는 내용과 함수의 반환값을 구하라.
int sum(int n)
{
printf("%d\n", n);
if(n<1) return 1;
else return(n+sum(n-1));
}출력 결과 및 반환 값
5
4
3
2
1
0
//반환값 : 16
int sum(5)
{
printf("%d\n", 5);
if (5 < 1) return 1;
else return(5 + sum(4));
}
...
int sum(4)
{
printf("%d\n", 4);
if (4 < 1) return 1;
else return(4 + sum(3));
}
...
int sum(3)
{
printf("%d\n", 3);
if (3 < 1) return 1;
else return(3 + sum(2));
}
...
int sum(2)
{
printf("%d\n", 2);
if (2 < 1) return 1;
else return(2 + sum(1));
}
...
int sum(1)
{
printf("%d\n", 1);
if (1 < 1) return 1;
else return(1 + sum(0));
}
...
int sum(0)
{
printf("%d\n", 0);
if (0 < 1) return 1; //return 1발생
else return(5 + sum(4));
}
sum(0) = 1
sum(1)=2
sum(2)=4
sum(3)=7
sum(4)=11
sum(5)=16 이므로 최종 반환값은 16이다8.
//다음 함수를 recursive(5)로 호출하였을 때, 화면에 출력되는 내용과 함수의 반환값을 구하라.
int recursive(int n) {
printf("%d\n", n);
if (n < 1) return 2;
else return(2 * recursive(n - 1) + 1);
}출력 결과 및 반환 값
5
4
3
2
1
0
이 출력 되며
int recursive(int 5) {
printf("%d\n", 5);
if (5 < 1) return 2;
else return(2 * recursive(4) + 1);
}
... //printf 결과 5 출력 ...
int recursive(int 4) {
printf("%d\n", 4);
if (4 < 1) return 2;
else return(2 * recursive(3) + 1);
}
...
int recursive(int 3) {
printf("%d\n", 3);
if (3 < 1) return 2;
else return(2 * recursive(2) + 1);
}
...
int recursive(int 2) {
printf("%d\n", 2);
if (2 < 1) return 2;
else return(2 * recursive(1) + 1);
}
...
int recursive(int 1) {
printf("%d\n", 1);
if (1 < 1) return 2;
else return(2 * recursive(0) + 1);
}
...
int recursive(int 0) {
printf("%d\n", 0);
if (0 < 1) return 2; //if조건에 충족해 return 2;
else return(2 * recursive(n - 1) + 1);
}
...
recursive(0)=2
recursive(1)=5
recursive(2)=11
recursive(3)=23
recursive(4)=47
recursive(5)=95
이므로 반환값은 95이다.9.
//다음 함수를 recursive(10)로 호출하였을 때, 화면에 출력되는 내용과 함수의 반환값을 구하라
int recursive(int n) {
printf("%d\n", n);
if (n < 1) return -1;
else return(recursive(n - 3) + 1);
}
출력 결과 및 반환 값
int recursive(int 10) {
printf("%d\n", 10);
if (10 < 1) return -1;
else return(recursive(7) + 1);
}
...
int recursive(int 7) {
printf("%d\n", 7);
if (7 < 1) return -1;
else return(recursive(4) + 1);
}
...
int recursive(int 4) {
printf("%d\n", 4);
if (4 < 1) return -1;
else return(recursive(1) + 1);
}
...
int recursive(int 1) {
printf("%d\n", 1);
if (1 < 1) return -1;
else return(recursive(-2) + 1);
}
...
int recursive(int -2) {
printf("%d\n", n);
if (-2 < 1) return -1; //if문 조건 충족으로 return -1
else return(recursive(n - 3) + 1);
}
recursive(-2)=-1
recursive(1)=0
recursive(4)=1
recursive(7)=2
recursive(10)=3
으로 출력 결과는 10 7 4 1 -2 이고 반환값은 3이다.10.
//다음 함수를 recursive(5)로 호출하였을 때, 화면에 출력되는 내용을 쓰시오
int recursive(int n) {
if (n != 1) recursive(n - 1);
printf("%d\n", n);
}출력 결과
int recursive(int 5) {
if (5 != 1) recursive(4);
printf("%d\n", n);
}
...
int recursive(int 4) {
if (4 != 1) recursive(3);
printf("%d\n", n);
}
...
int recursive(int 3) {
if (3 != 1) recursive(2);
printf("%d\n", n);
}
...
int recursive(int 2) {
if (2 != 1) recursive(1);
printf("%d\n", n);
}
...
int recursive(int 1) {
if (1 != 1) recursive(2);
printf("%d\n", n);
}
...
이렇게 호출한후 recursive(1)부터 recursive(5)까지 순환한다.
고로 recursive(1)의 출력 값 1부터 차례대로 1,2,3,4,5 출력 된다.11.
//다음 함수에서 asterisk(5)를 호출할 때 출력되는 *의 갯수는?
void asterisk(int i) {
if (i > 1) {
asterisk(i / 2);
asterisk(i / 2);
}
printf("*");
}출력 결과
*******로 7개다
굉장히 복잡했다.. 코드가 간단해 보였는데
먼저 asterisk(5)를 호출하면 if문에 걸려
asterisk(2)가 생성 된다
그 asterisk(2)가 호출되어서 asterisk(1)이 호출이 된다.
asterisk(1)은 if조건에 맞지 않으므로 첫번째 *이 출력이 된다.
그 후 다시 asterisk(2)를 처리해야하는데
조건에 의해 (i/2) 후 asterisk(1)이 호출되어 두번째 *이 출력이 된다.
그후 다시 asterisk(2)가 두번째(i/2) 계산으로 asterisk(1)이 호출되고 세번째 *이 출력이 된다.
그렇게 asterisk(5)에 대한 첫번째 (i/2)가 끝났다.
두번째 (i/2)로 asterisk(2)가 나오고 그로인해 asterisk(1)으로 네번째 *이 출력이 된다
asterisk(2)에 대한 (i/2)로 다섯번째 *이 출력이 된다.
asterisk(2)에 대한 두번째(i/2)로 여섯번째 *이 출력이 된 후 asterisk(5)에 대한 두번째(i/2)로 인해
마지막 *이 출력 되며 총 출력 개수는 7개 이다.위에는 그냥 말도 어렵고

이렇게 이해하면 쉽다! 난 왜 이런 생각 못했을까 지훈이형 고마워
12.
//다음과 같은 함수를 호출하고 "recursive" 문자열을 입력한 다음, 엔터키를 눌렀다면 화면에 출력되는 것은?
unknown() {
int ch;
if ((ch = getchar(1)) != '\n') {
unknown(1);
}
putchar(ch);
}출력 결과
evisrucer
r ->unknown 순환
..
..
e
c
r
u
s
i
v
e
e 다음 \n이므로 putchar 함수 실행 되면서 스택중 가장 위에 있는 e부터 순환하며 출력13.
//1+2+3+...+n을 계산하는 순환적인 프로그램을 작성하시오
int sum(int n) {
if (n == 1) {
return 1;
}
return n + sum(n - 1);
}
int main(void) {
int a = sum(5);
printf("%d", a);
}출력 결과
15매우 쉬운 문제였다..!!
14.
//1+1/2+1/3+...+1/n을 계산하는 순환적인 프로그램을 작성하시오
int sum(int n) {
if (n == 1) {
return 1;
}
return (double)1/n + sum(n-1);
}재귀함수는 진짜 종료조건, 핵심키워드만 찾으면 끝인거 같다.
15.
//순환호출 되는 것을 이해하기 위하여 fib함수를 다음과 같이 바꾸어서 실행하여 보라.
//fib(6)을 호출할 때 화면에 출력되는 내용을 쓰시오.
int fib(int n)
{
printf("fib(%d) is called\n", n);
if(n==0) return 0;
if(n==1) return 1;
return (fib(n-1)+fib(n-2));
}출력 결과
fib(6) is called
fib(5) is called
fib(4) is called
fib(3) is called
fib(2) is called
fib(1) is called
fib(0) is called
fib(1) is called
fib(2) is called
fib(1) is called
fib(0) is called
fib(3) is called
fib(2) is called
fib(1) is called
fib(0) is called
fib(1) is called
fib(4) is called
fib(3) is called
fib(2) is called
fib(1) is called
fib(0) is called
fib(1) is called
fib(2) is called
fib(1) is called
fib(0) is called위의 과정을 그림으로 나타낸 것이다.

그림으로 보니까 훨씬 이해가 쉽게 되지 않나? 아무튼 뿌듯하다..
16.
//순환적인 프로그램을 반복 구조를 사용한 비순환적 프로그램으로 바꾸시오.
int sum(int n)
{
if(n==1) return 1;
else return(n+sum(n-1));
}이를 잘 살펴보면 n이 5라고 가정하였을때 5+4+3+2+1으로 1부터 n까지의 합을 더하는 것이 핵심 키워드이다.
int sum(int n)
{
int tmp = 0;
for (int i = 1; i <= n; i++) {
tmp += i;
}
return tmp;
}
int main(void) {
int a =sum(10);
printf("%d", a);
}
//을 출력하면 정상적으로 55가 출력 되는 것을 확인할 수 있다.17.
//이항계수를 계산하는 순환함수를 작성하라. 이항계수는 다음과 같이 순환적으로 정의 된다.
//반복함수로도 구현해보라.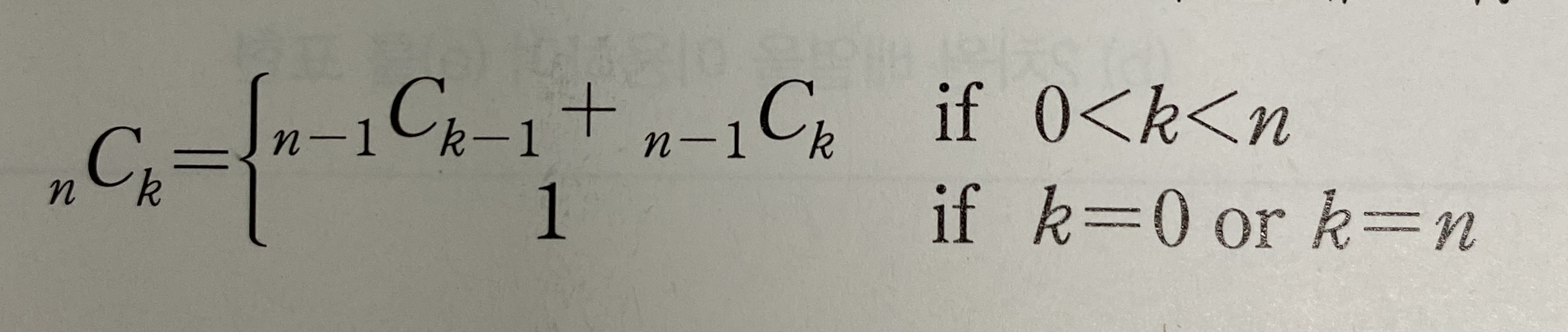
//순환
int C(int n, int k) {
if (k == 0 || k == 1) {
return 1;
}
return C(n - 1, k - 1) + C(n - 1, k);
}반복은 패스 ... 아직 못하겠다
18.
//Ackermann함수는 다음과 같이 순환적으로 정의 된다.
A(0, n) = n+1
A(m, 0) = A(m-1, 1)
A(m, n) = A(m-1, A(m, n-1)) m,n>=1
(a)A(3,2)와 A(2,3)의 값을 구하시오
(b)이를 순환적인 프로그램으로 작성하시오
(c)위 순환적인 프로그램을 반복문을 이용해 비순환적 프로그램으로 바꾸시오(a) Ackerman(3,2)의 값 : 29
Ackerman(2,3)의 값 : 9
(b)
int Ackermann(m, n) {
if (m == 0) {
return n + 1;
}
else if (n == 0) {
return Ackermann(m - 1, 1);
}
else {
return Ackermann(m - 1, Ackermann(m, n - 1));
}
}
(c)는 나중에..19.
//본문의 순환적인 피보나치 수열 프로그램과 반복적인 피보나치 수열 프로그램의 수행 시간을 측정하여
//비교하라. 어떤 결론을 내릴 수 있는가?
먼저 순환 피보나치 수열의 알고리즘을 보면
T(n) = T(n-1)+T(n-2)+C이다.
대략 계산해보면 순환 피보나치 수열의 시간 복잡도는 O(2^n)이다.
이 시간 복잡도의 패턴은
fib(6)을 호출 하였을때
fib(5) 1회
fib(4) 2회
fib(3) 3회
fib(2) 5회
fib(1) 8회 이다.
반복을 이용한 피보나치 수열 계산 프로그램은 n번째 값을 구하는데 (n-1)의 연산만 필요하다
이 프로그램의 시간 복잡도는 O(n)이다.
O(n)과 O(2^n)의 수행시간은 O(n)이 훨씬 빠르기에 피보나치 수열의 경우 순환보다 반복을 이용해
작성하는 것이 효율적이라고 말할 수 있다.20.
//순환호출에서는 순환호출을 할때마다 문제의 크기가 작아져야 한다.
(1)팩토리얼 계산 문제에서 순환호출이 일어날 때마다 문제가 어떻게 작아지는가?
A :
int factorial(int n)
{
if(n<=1) return 1;
else return n * factorial(n-1)
}
위의 구문과 같이 n이 호출될때마다 n-1 <-이 함수가 호출이 되면 n-2 ...형식으로 n이 1씩 작아진다.
(2)하노이의 탑에서 순환호출이 일어날 때마다 문제가 어떻게 작아지는가?
A : 아직 잘모르겠어
'C' 카테고리의 다른 글
| C - call by value / call by reference (0) | 2022.04.05 |
|---|---|
| C - 자료구조 배열/구조체/포인터/동적 메모리 할당 (0) | 2022.04.05 |
| C - 자료구조 순환 (0) | 2022.03.23 |
| C - Big-O 표기법 (0) | 2022.03.22 |
| C - 자료구조 성능과 점근적 분석법 (0) | 2022.03.21 |