Algorithm - Tree
2022. 10. 20. 14:21ㆍAlgorithm
Tree
계층적인 구조를 나타내는 자료구조
트리의 용어
노드(node) : 트리의 구성요소
루트(root) : 부모가 없는 노드
서브트리(subtree) : 하나의 노드와 그 노드들의 자손들로 이루어진 트리
단말노드(terminal node) : 자식이 없는 노드
비단말노드 : 적어도 하나의 자식을 가지는 노드
자식, 부모, 형제, 조상, 자손 노드 : 인간과 동일
레벨(level) : 트리의 각층 번호 최상위 경우 level 1 그 자식은 level 2, level 2의 자식은 level 3
높이(height) : 트리의 최대 레벨(3)
차수(degree) : 노드가 가지고 있는 자식 노드의 개수
트리의 값 저장 방식
1. 데이터와 연결 상태를 저장할 클래스 공간(=노드) 생성
public static class Node {
Object data; //저장할 값
Node left; //왼쪽 노드
Node right; //오른쪽 노드
}2. 각각의 노드들에 값 저장

3. 노드 간 연결 상태 정의
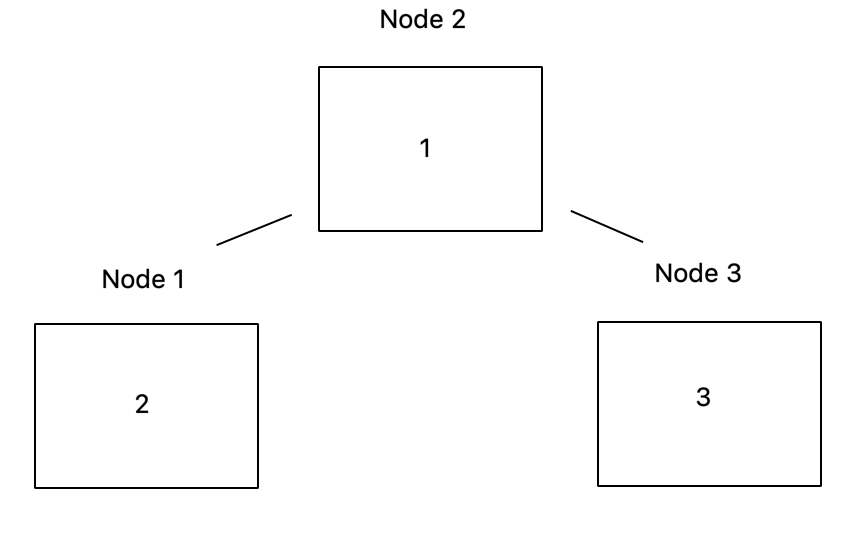
이를 코드로 나타내면
//2번 과정
Node node1 = tree.addNode(5);
Node node2 = tree.addNode(3);
Node node3 = tree.addNode(2);
//3번 과정
node2.addLeft(node1);
node2.addRight(node3);
이진트리
- 이진트리는 자식 노드가 최대 2개인 트리를 의미한다.
- 노드의 개수가 n개이면 간선의 개수는 n-1
- 높이가 h인 이진트리의 경우, 최소 h개의 노드를 가지며 최대 2^h-1개의 노드를 가진다.
- n개의 노드를 가지는 이진트리의 높이는 최대 n이거나 최소 [log2(n+1)]
트리의 순회 방법
트리의 순회 방법으로는 전위(pre-order), 중위(in-order), 후위(post-order) 3가지가 있다.
- 전위 순회 : 루트 노드를 먼저 순회한 후, 왼쪽 하위 -> 오른쪽 하위 순으로 순회
- 중위 순회 : 왼쪽 가장 하위 노드를 먼저 순회한 후, 바로 상위 노드 -> 오른쪽 하위 순으로 순회
- 후위 순회 : 왼쪽 가장 하위 노드를 먼저 순회한 후, 오른쪽 하위 노드 -> 바로 상위 노드 순으로 순회
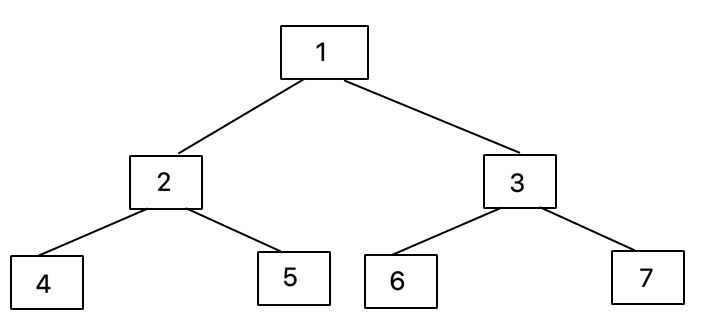
전위 순회 : 1-2-4-5-3-6-7
중위 순회 : 4-2-5-1-6-3-7
후위 순회 : 4-5-2-6-7-3-1
트리의 구현
package Algorithm;
public class Tree{
static int count;
public Tree() {
count = 0;
}
public static class Node {
Object data; //노드에 저장할 값
Node left; //왼쪽 노드
Node right; //오른쪽 노드
public Node(Object data) {
this.data = data; //Node 생성시 매개변수로 넣은 data를 저장
left = null;
right = null;
//어떤 노드에도 연결되어 있지 않은 상태
}
public void addLeft(Node node) { //노드의 왼쪽에 다른 노드를 연결
left = node;
count++; //연결된 노드 수 1 증가
}
public void addRight(Node node) { //노드의 오른쪽에 다른 노드를 연결
right = node;
count++; //연결된 노드 수 1 증가
}
public void deleteLeft() { //왼쪽 노드를 삭제
left = null; //Node.left가 null을 가리키게 하여 기존 LeftNode는 사라짐
count--; //연결된 노드 수 1 감소
}
public void deleteRight() { //오른쪽 노드를 삭제
right = null; //Node.right가 null을 가리키게 하여 기존 RightNode는 사라짐
count--; //연결된 노드 수 1 감소
}
}
public Node addNode(Object data) { //새로운 노드 생성
Node n = new Node(data); //data 값을 가지고 있는 노드를 생성
return n; //Node n 반환
}
public void preOrder(Node node) { //전위 순회
if(node == null) { //만약 노드가 null 값을 가질 경우 종료
return;
}
//전위 순회는 루트노드를 먼저 방문 -> 완쪽 노드 방문 -> 오른쪽 노드 방문
System.out.print(node.data + " ");
preOrder(node.left);
preOrder(node.right);
}
public void inOrder(Node node) { //중위 순회
if(node == null) { //만약 노드가 null 값을 가질 경우 종료
return;
}
//중위 순회는 왼쪽 노드를 먼저 방문 -> 중앙 노드 방문 -> 상위 노드 방문
inOrder(node.left);
System.out.print(node.data + " ");
inOrder(node.right);
}
public void postOrder(Node node) { //후위 순회
if(node == null) { //만약 노드가 null 값을 가질 경우 종료
return;
}
//후위순회는 왼쪽 노드를 먼저 방문 -> 오른쪽 노드 방문 -> 상위 노드 방문
postOrder(node.left);
postOrder(node.right);
System.out.print(node.data + " ");
}
public static void main(String[] args) {
// 트리 생성
Tree tree = new Tree();
// 노드 생성
Node node1 = tree.addNode(1);
Node node2 = tree.addNode(2);
Node node3 = tree.addNode(3);
Node node4 = tree.addNode(4);
Node node5 = tree.addNode(5);
Node node6 = tree.addNode(6);
Node node7 = tree.addNode(7);
// 트리 연결관계 생성
/* 트리 모양
* 1
* 2 3
* 4 5 6 7
*/
node1.addLeft(node2);
node1.addRight(node3);
node2.addLeft(node4);
node2.addRight(node5);
node3.addLeft(node6);
node3.addRight(node7);
// 순회
tree.preOrder(node1);
System.out.println();
tree.inOrder(node1);
System.out.println();
tree.postOrder(node1);
System.out.println();
// 삭제
node2.deleteLeft();
node3.deleteRight();
/* 삭제 이후 트리 모양
* 1
* 2 3
* 5 6
*/
// 순회
System.out.println();
tree.preOrder(node1);
System.out.println();
tree.inOrder(node1);
System.out.println();
tree.postOrder(node1);
System.out.println();
System.out.println("노드 갯수"+ count);
}
}출력 결과
1 2 4 5 3 6 7
4 2 5 1 6 3 7
4 5 2 6 7 3 1
1 2 5 3 6
2 5 1 6 3
5 2 6 3 1'Algorithm' 카테고리의 다른 글
| Algorithm - Graph (0) | 2022.10.20 |
|---|---|
| Algorithm - 우선순위 큐(Priority Queue) (0) | 2022.10.20 |
| Algorithm - 1주차 (0) | 2022.10.14 |
| 시간복잡도에 관한 구체적이고 쉬운 이야기 (1) | 2022.09.30 |
| Algorithm - 정렬 알고리즘 (0) | 2022.09.16 |