Algorithm - Graph
2022. 10. 20. 17:30ㆍAlgorithm
Graph
객체들의 쌍들이 서로 연관되어 객체의 집합을 이루는 자료구조
사물/추상적인 개념간의 연결 관계를 표현한 것
그래프란?
- 트리도 그래프의 특수한 경우
- 큰 프로젝트에서 작은 프로젝트 간의 우선 순위
- 도시들의 연결 상태
- 지하철 노선도
그래프의 구성요소
- 정점(Vertex/Node) : 그래프에서의 위치
- 여러가지 특성을 가질 수 있는 객체를 의미
- V(G) : 그래프 G의 정점들의 집합
- 간선(Edge/Link/Branch) : 그래프에서 위치간의 관계
- 정점(노드)를 연결하는 선
- E(G) : 그래프 G의 간선들의 집합
- 인접 정점(Adjacent Vertex) : 간선(Edge)에 의해 직접 연결된 정점을 의미
- G(V, E) : 그래프는 정점과 간선의 집합이므로 G(V, E)는 그래프 자체를 의미
그래프의 종류
- 무방향 그래프(undirected graph)
- 무방향 간선으로만 사용
- 간선을 통해서 양방향으로 갈 수 있음
- (A, B) = (B, A)
- 위와 같이 정점의 쌍으로 표현
- 무방향 그래프의 모든 차수의 합은 간선 수의 2배
- 방향 그래프(directed graph)
- 방향 간선(undirected edge)만 사용
- 간선을 통해서 한쪽 방향으로만 갈 수 있음
- <A, B>와 같이 정점의 쌍으로 표현
- <A, B> != <B, A>
- 가중치 그래프
- 간선에 비용(cost) or 가중치(weight)가 할당된 그래프
- 서면역->노포역일 경우 정점은 서면, 노포이며 그 사이를 연결하는 길이 간선 가중치는 그 도로의 길이이다.
- 간선에 비용(cost) or 가중치(weight)가 할당된 그래프
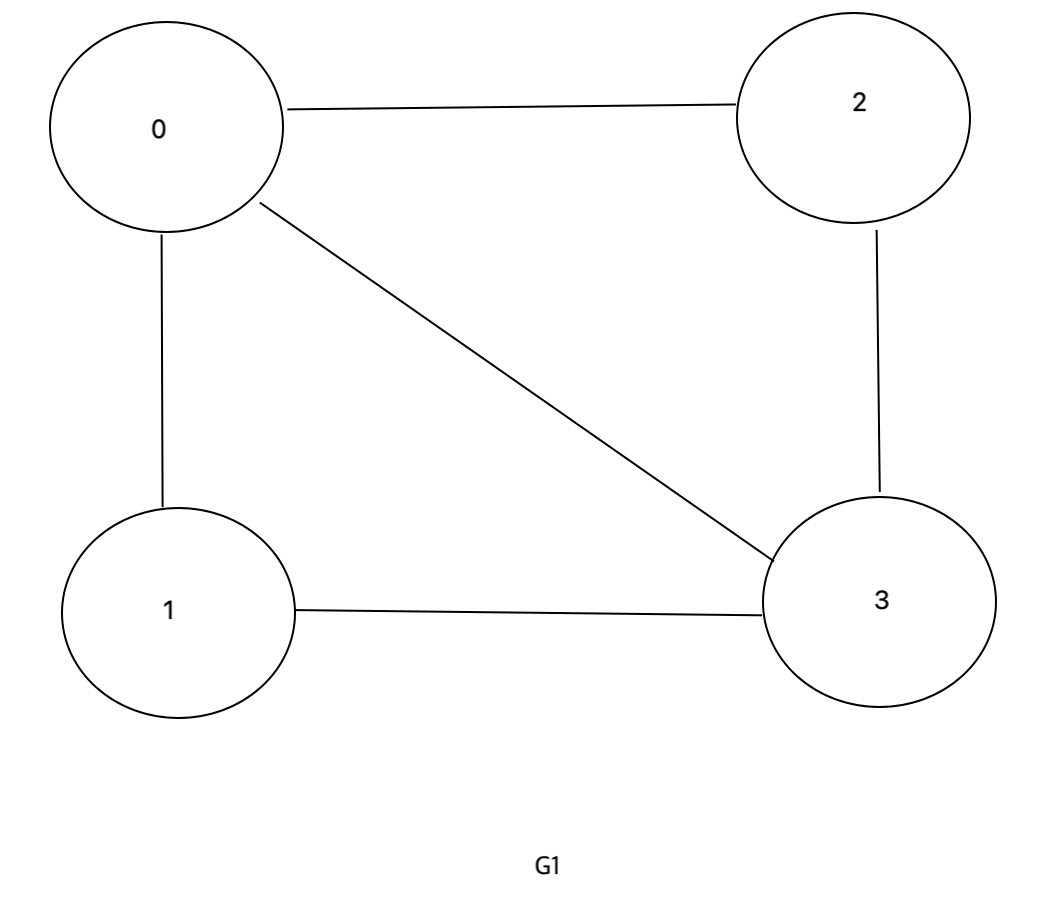
위 그래프 표현을 예시로 들면
V(G1) = {0,1,2,3}, E(G1) = {(0,1), (0,2), (0,3), (1,2), (2,3)}
- 부분 그래프
'Algorithm' 카테고리의 다른 글
| Algorithm - Dynamic Programming (0) | 2022.11.03 |
|---|---|
| Algorithm - Hash (0) | 2022.10.27 |
| Algorithm - 우선순위 큐(Priority Queue) (0) | 2022.10.20 |
| Algorithm - Tree (0) | 2022.10.20 |
| Algorithm - 1주차 (0) | 2022.10.14 |